続いて、「確率そのものをツールとするアルゴリズム」に目を転じていきます。
「ベイズの定理」にもとづく「ベイズ推定」や「ベイズ改訂」の話が中心になります。ただ、ベイズの定理を示したトーマス・ベイズは1702年生まれの18世紀の人。ベイズ推定やベイズ改訂はベイズの死後考案されたものでしたが、いずれにせよ出所は人工知能と何の関係もありません。
関係はなかったのですが、ベイズ推定という確率計算は、問題がほんの少し複雑になるだけでも計算量が膨大になり、例の「組み合わせ爆発」にも似た計算困難度に達するものです。そのため、現代に入ってコンピュータが発達し、超高速演算ができるようになったため、ようやく実用的になりえたというところがあります。
古典的な考え方の枠組み
ベイズ推定に入る前に、もっと古い思考の枠組みを簡単に押さえておきます。これは、アルゴリズムというよりも、「思考の経済」、「思考の節約」とでも言うべきものです。
ひとつは「オッカムの剃刀」です。14世紀の修道士、オッカムのウィリアムが残した言葉が元になっています。「剃刀(カミソリ)」は説明に不要な要素を切り落とすことをたとえており、「ある事柄を説明するために、必要以上に多くの仮定を立てるべきではない」とする指針です。「ある事柄に対する説明については、仮定がより少ないものがすぐれている」など、似たような意味のバリエーションがいくつかあります。
もうひとつはさらに古く、紀元前4~3世紀のエピクロスによる「複数説明の原理」です。こちらは「複数の理論が観察に合致するなら、すべての理論を保持せよ」とします。オッカムの剃刀の正反対ですね。
今まで出てきた人工知能技術アルゴリズムに当てはめれば、オッカムの剃刀はヒューリスティックな試行の選択、複数説明の原理は局所最適解におちいるリスクの回避につながる考え方と言えるでしょう。ベイズ推定は、「○○が××である確率は~%」、「○○が××した確率は~%」などといった出力を返すアルゴリズムです。「○○が××である確率は~%」というのは、言い換えれば「○○が××でない確率は(100-~)%」ということですから、確率の低い方の可能性も完全に切り捨ててはいないのです。つまり、オッカムの剃刀と複数説明の原理の両方をバランス良く取り込むことができる考え方と言えます。
モンティ・ホール問題
ベイズ推定の話につながる面白い話から見ていきましょう。モンティ・ホールという人が司会を務めるアメリカのゲームショー番組で実際に行われていたゲームがきっかけとなった騒動です。ですからノンフィクションです。
そのゲームはこのようなものでした。
「プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が(当たり)、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。ここでプレーヤーは、最初に選んだドアを、残りの開けられていないドアに変更してもよいと言われる。」
ここで問題になるのが、「プレーヤーは、ドアを変更した方が得かどうか」です。
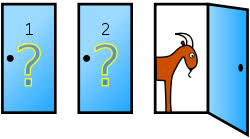
1990年9月9日発行のニュース雑誌「パレード」で、マリリン・ヴォス・サヴァントという人がこの問題に対し「正解は『ドアを変更する』である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と回答しました。すぐにこれに対する読者からの投書が殺到しました。大部分が「その答えは間違っている!当たりの確率は五分五分のままだ!」とするもので、中には博士号保持者や高名な数学者からの反論もありました。サヴァントは殺到する反論に対して屈することなく、翌年にかけて3回も「パレード」誌上のコラムで反反論します。
そうこうするうち、アンドリュー・ヴァージョニという人がPCを使ってモンテカルロ法によるこの問題のシミュレーションを行いました。その結果、ドアを変えなかった場合の勝率は3分の1、ドアを変えた場合の勝率は3分の2に収束していく傾向がはっきりと表され、サヴァントの答えが正しかったことが示されたのです。
では、どうしてドアを変えると勝率が3分の2になるのか、見ていきましょう。
このゲームには、いくつか暗黙のルールがあります。それを整理すると、
(1) 3つのドア (A, B, C) に(景品、ヤギ、ヤギ)がランダムに入っている。
(2) プレーヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。
となります。
このゲームについて言えるまず言えることは、「プレーヤーが最初に当たりのドアを選ぶ確率は3分の1、はずれのドアを選ぶ確率は3分の2である」ということです。場合分けをして考えます。
① 最初に当たりのドアを選んでいる場合
3分の1の確率で、プレーヤーは当たりのドアを選びます。モンティは残り2つのドアのどちらかを開け、ヤギを見せる。この場合、開かれていないドアにもヤギがいるため、ドアを変更しなければ当たり、変更すればはずれ。
〇・変更しない →勝率は最初の選択時点と変わらず、3分の1
〇・変更する →勝率はゼロ
という勝率になります。
② 最初にはずれのドアを選んでいる場合
3分の2の確率でプレーヤーははずれのドアを選びます。モンティは残り2つのドアのうち、ヤギがいる方を必ず開けます。すると、
〇・変更しない →勝率はゼロ
〇・変更する →勝率100%
です。
①と②を合わせた全体的勝率は、
・変更しない ![]()
・変更する ![]()
となります。
ヤギを区別して考えてみる
わかりにくいかもしれません。少し視点を変えて、ヤギにオスとメスがいると考えて場合分けします。
最初の選択 残りのドアの中身
↓ ↓
ケース① 新車 / ヤギ♂ ヤギ♀
ケース② ヤギ♂ / 新車 ヤギ♀
ケース③ ヤギ♀ / ヤギ♂ 新車
ここで、最初に当たりを引けるケースは1つ(①)、はずれを引くケースは2つ(②と③)あります。
モンティがヤギを見せたあと、ドアを変更した場合、ケース①では勝率ゼロ、ケース②と③ではどちらも100%です。
モンティがヤギを見せたあと、ドアを変更しない場合、ケース①では勝率100%、ケース②と③ではどちらも0%です。
「ドアを変更する」ならば全ケースでの勝率は 200/300=2/3 となり、「ドアを変更しない」ならば全ケースでの勝率は 100/300=1/3 となります。
「最初にはずれを引くケースの方が1つ多い」ことを見落としてしまうと、ドアを変える/変えない後の確率が50%:50%に思えてしまう……というところがワナなのです。
ドアの数を増やしてみる
もっと極端な状況を想定して考えても、わかりやすいかもしれません。
ドアは1000個あります。新車が1台、いずれかのドアの向こうにあり、残り999のドアの背後にはヤギがいます。スタジオがかなり獣臭くなるかもしれません。中には勝手に交尾をはじめるヤギも……なんていう想像は置いておきまして、プレーヤーはドアをひとつ選びます。
するとモンティは、ヤギがいる998個のドアを開いてヤギを見せます。もはや開いていないのは2つだけで、そのうちひとつはプレーヤーが選んだものです。
プレーヤーが最初にひとつのドアを選んだとき、そのドアに新車がある確率はたったの1000分の1でした。「まず、ないな」という確率、というか「ヤギ率1000分の999=99.9%」です。ところがモンティが998個のドアを開けた後となると、最初に選んだドアは「新車率0.01%・ヤギ率99.9%」のままですが、もうひとつのドアは「新車率99.9%・ヤギ率0.01%」にはね上がっているのです。これはもう、そのドアを選び直すに決まってますよね。
さて、モンティ・ホールの話が長くなってしまいましたので、ベイズ推定については次の記事で見ていくことにしましょう。