統計的手法と重なる部分も大きいのですが、「確率」もまた、人工知能技術によく用いられます。ひとつ前の「統計」のカテゴリーですでに出してしまったニューラルネットワークですが、やっていることは「認識対象データの特徴を、確率分布としてとらえていく」ことですので、もうすでにここに確率が関係しています。この点は、ニューラルネットワークの源流のひとつである制限ボルツマンマシン Restricted Boltzmann Machine から変わっていません。
人工知能技術と確率
それに、そもそも確率は人工知能研究の最初から深く関わってきます。1951年のSNARCは、信号がある真空管を通る確率を高くしたり低くしたりすることを通じて迷路の脱出経路を学習させるものでした。
また、遺伝的アルゴリズムや焼きなまし法でも、それぞれ突然変異、探索解空間の大幅な変更などといった局所最適解におちいる危険回避のためのステップは、設定された確率で起きるようにされていましたね。
確率と人工知能の関わりはこれほど深いのですが、もっと直接的に確率をアルゴリズムに活用した人工知能技術もあります。大きくわけて、
・エージェントに確率的に振る舞わせる(遺伝的アルゴリズム、焼きなまし法)
・確率そのものをアルゴリズムのツールにする
というふたつの方向があります。
乱択アルゴリズム
「エージェントに確率的に振る舞わせる」方式は、まとめて乱択アルゴリズムと呼ばれます。上記のように遺伝的アルゴリズムや焼きなまし法が含まれていますが、これらよりももっと確率まかせにして、ほとんど「解のランダム探索」と言えるほどのものがあります。
・モンテカルロ法
そのような「解のランダム探索」といえる計算アルゴリズムにモンテカルロ法があります。モンテカルロ法はずいぶん昔からあり、人工知能技術ではありません。しかし、密接に関連してくる方法のひとつですので紹介しておきたいと思います。
モンテカルロ法は、乱数を用いて多数回の試行を重ね、その試行の結果算定されてくる確率が解に近似していくのを利用する方法です。
たとえば、モンテカルロ法で円周率を計算してみましょう。下のような正方形に円が内接している図を考えます。円の半径は1、正方形の1辺は2の長さです。すると、円の面積は1×1×円周率(π)ですからπ、正方形の面積は4と表されます。
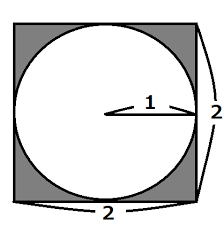
ここで乱数の登場です。この正方形内にまんべんなく、ランダムに点を打っていきます。そのとき、円内に点が打たれたら1点、円外の灰色の範囲に打たれたら0点をカウントしていきます。こういうルールで、何万回も点を打っていきます。
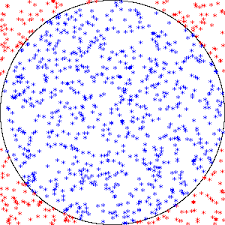
そうしますと、円内に収まった点の数だけ得点が入りますから、
打ったすべての点(N):円内に収まった点(P)=4:π
となり、これを変形すると、
![]()
となります。得点を4倍して試行回数Nで割った答えが円周率の近似値になり、近似の精度は試行回数が増えるほど高くなることが期待できます。
逆に言うと、円内に点が打たれる という確率そのものが円周率(の4分の1)を表しているのです。
このように、乱数を使って確率で近似解を求めるのがモンテカルロ法です。
・強化学習
機械学習のモンテカルロ法が、強化学習です。エージェントにランダムに行動させ、環境の変化が好ましいものであれば報酬を与え、その行動をとる確率を高め、好ましくない変化を引き起こした行動には無報酬かマイナスの報酬を与え、その行動をとる確率を低くする……という流れで最適解を探索させます。
こちらで触れていますが、強化学習はけっこう力任せの強引な機械学習の方式です。また、こちらのサイトでは、障害物をかわしながら目的地までの最短ルートを探索する強化学習アルゴリズムを視覚的に体験できるようになっています。クリックすると障害物を追加できますので、いろいろやってみてください。
Youtube なんかでも、強化学習でコンピュータがテトリスにだんだん強くなっていったり、シューティングゲームで神ってる感じになったりする映像が見られるでしょう。こちらは「強化学習で二足歩行を学習させる」試みですが、狂気を感じさせるテイストが何とも言えません。
以上のようなものを見ていただければ感覚的にわかると思いますが、本当に力任せで、5万回とか10万回といった学習を経て、ようやく上達していきます。効率がいいとは決して言えず、コンピュータの超高速演算があるから(そして映像では編集により経過の一部しか紹介されていないから)一応まともに見られる結果になっているだけです。
ただ、現実に成果を上げているのは事実で、チェスや碁などのゲームでは人間にマシンが勝てるようになってきていることには、この強化学習がかなり大きく貢献しています。
また、強化学習は「とにかく場数を踏んでうまくいったやり方を覚えろ」という方式ですので、環境が多少変化しても対応していけるところがあります。遺伝的アルゴリズムだと、環境が変わると最初からやり直すのと同じ手間ひま、コストをかけることになりますが、強化学習は放っておくだけでほとんど大丈夫です。
これらが「エージェントに確率的な振る舞いをさせ、最適解を探索させる」アルゴリズムです。トライ&エラーの繰り返しで解決の道を探索していく点では、これらもヒューリスティックであることがおわかりいただけると思います。
続いては、「確率そのものをツールとして推論するアルゴリズム」です。