ではベイズ推定の話に入ります。まずは「ベイズの定理」から。
ベイズの定理
ベイズの定理は決して難しくありませんが、「ベイズ推定」につながるきわめて強力なツールを与えてくれます。まずはこれを押さえましょう。
ベイズの定理であつかうのは、「○○が起きたもとで××が起きた確率」という条件付き確率です。下のベン図を見ながら考えていきましょう。
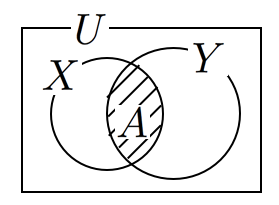
P(X)：「Xが起きる確率」をこのように書きます。ベン図で整理すると以下のようになります。
P(Y|X)：「Xが起きて、かつYが起きる確率」です。以下のようになります。
つまり「XもYも起きる確率(A)」は、「Xが起きる確率」×「Xが起きて、かつYが起きる確率」で計算されるので、
P(X∩Y)＝P(X)P(Y|X) が成り立ちます。ベン図でいうと以下。
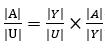
さてここで、同じことをYの側から考えるのです。すなわち、
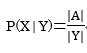P(X∩Y)＝P(Y)P(X|Y)
ベン図では
が成り立ちます。
すると、
P(X)P(Y|X)＝P(Y)P(X|Y)
という恒等式が成立します。これがベイズの定理です。「XもYも起きる確率」をふた通りの方法で表したものです。
これを使うと、P(X)、P(Y|X)、P(Y)、P(X|Y)の4つのうち3つがわかっていれば残りの1つも算定できることになります。が、ふつうは条件付き確率を求めるのが目的となるので、
とか、
といった形で使うことが多くなります。
ここでP(X)やP(Y)のことを「事前確率」、P(Y|X)やP(X|Y)は「Xが起きたことがわかったうえでのYの事後確率」、「Yが起きたことがわかったうえでのXの事後確率」といいます。そして、P(Y|X)を求めるためのP(X|Y)や、P(Y|X)を求めるためのP(X|Y)を「条件確率」、「尤度（ゆうど）」といいます。
モンティ・ホール問題にあてはめてみる
では、上のような式をモンティ・ホール問題に応用してみましょう。
ドア①、②、③があるとします。プレーヤーは最初、ドア①を選びました。モンティはドア②を開け、ヤギを見せました。このケースで、
・モンティがドア②を開けた後、ドア①に新車がある確率
・モンティがドア②を開けた後、ドア③に新車がある確率
をそれぞれ求めます。
・モンティがドア②を開けた後、ドア①に新車がある確率
P(Y|X)：ドア②が開いた後で、ドア①に新車がある確率→求めたいのはコレ
P(X) ：ドア②が開く確率→ 1／2
P(Y) ：ドア①に新車がある事前確率→ 1／3
P(X|Y)：ドア①に新車があった場合に、ドア②を開く確率（条件確率：尤度）→モンティは②も③も開けられるので 1／2
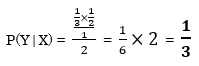
・モンティがドア②を開けた後、ドア③に新車がある確率
P(Y|X)：ドア②が開いた後で、ドア③に新車がある確率→求めたいのはコレ
P(X) ：ドア②が開く確率→ 1／2
P(Y) ：ドア③に新車がある事前確率→ 1／3
P(X|Y)：ドア③に新車があった場合に、ドア②を開く確率（条件確率：尤度）→ 1／1 (①はプレーヤーが選んでおり、③には新車があるので、モンティは②を開くしかない)
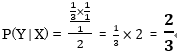
……ということで、プレーヤーがドア①を選び、モンティがドア②を開けたあとで、ドア①に新車がある確率は3分の1、ドア③に新車がある確率は3分の2と出ました。
ベイズ推定
上記のように、ベイズの定理で得られた式を用いて条件付き確率を求める計算が「ベイズ推定」です。
では、モンティ・ホール問題とはまた別の例で、もう一度見てみましょう。ベイズ統計学の参考書でとてもよく見かける例題で、少し気持ちが明るくなる話です。
〇ある検査を受けたとき、被験者がガンであるときに陽性となる確率は95％、ガンでないが陽性と誤判定する確率は2％とする。また、ガンの罹患率は0.1％とする。この条件下において、検査結果が陽性ならばガンである確率はいくらか？
こういう問題です。
まず、出てくる各種の確率を定義し、式に表します。
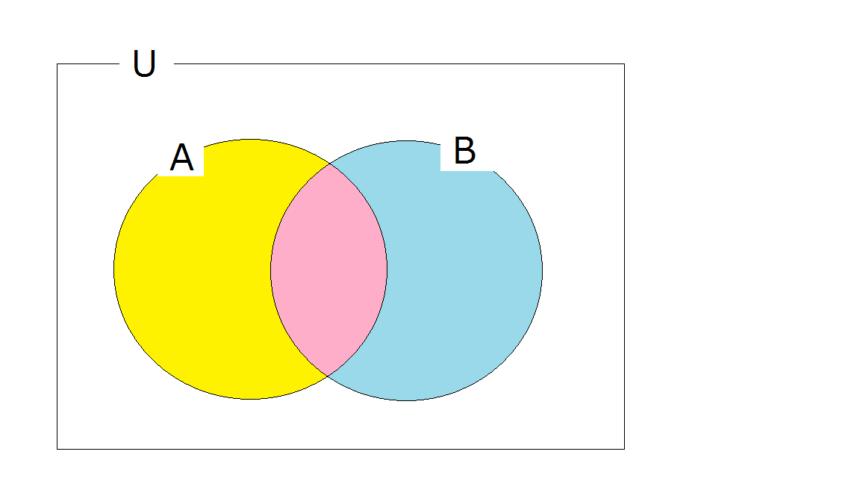
「ガンである」という事象 → A
「検査で陽性となる」事象 → B
「ガンであるときに陽性となる確率（尤度）」 → P(B|A)= 95／100
「ガンではないが陽性と誤判定する確率」 → P(B|Ā)= 2／100
「ガンの罹患率」 → P(A)= 1／1000
「陽性で実際にガンである確率」 → P(A|B) ……これが求めたい確率です。
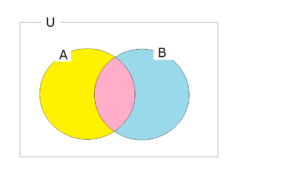
ここで少しややこしいのは、「検査で陽性となる確率 P(B)」は、「ガンであって陽性となる確率」と「ガンではないのに陽性と誤判定する確率」を両方含んでいるということです（ふたつの確率の和です）。
「ガンであって陽性となる確率」は「ガンである確率 P(A)」のうちの「ガンであって陽性となる確率」ですので、上のベン図でいうとピンク色の領域です。この領域の確率は、「黄色＋ピンク領域」の中での「ピンク領域の確率」ですので、この両者の積、P(A)×P(B|A)と表されます。数値では 1／1000×95／100 です。
そして「ガンではないのに陽性と誤判定する確率」は、上のベン図ではブルーの領域です。この領域の確率は、Aの円の外側すべて（白＋ブルーの領域）の確率（1－1／1000＝999／1000）と青の領域との積、P(Ā)×P(B|Ā)と表されます。数値では 999／1000×2／100 となります。
「検査で陽性となる確率 P(B)」（ピンク＋ブルー）は、ピンク・P(A)P(B|A)とブルー・P(Ā)P(B|Ā)の和となりますので、
となります。これを分母にしてピンク領域・P(A)P(B|A)を割り算してやれば、答えがでます。
ざっと4.5％といった数字になるわけです。
つまり、検査で陽性と出たけれども、ちゃんと精密検査してみて本当にガンである確率はたったの4.5％ということです。
実際に100万人いると想定して確認してみましょう。
罹患率0.1％ですから、そのうちガンの人は1000人です。検査を受けますと、この1000人のうち950人が陽性になります。
一方、99万9000人はガンではありませんが、検査を受けると2％の1万9980人が陽性になります。
1万9980人＋950人＝2万930人が陽性となっていますが、このうち本当にガンの人は950人だけということです。950÷20930を計算すると、上の数字に合致します。
ベイズ改訂
さて、上の100万人を想定した例では、50人、ガンなのに無罪放免となった人もいることがおわかりいただけると思います。わずかとはいえ、ちょっとこわいですね。
そこで、検査方法が改善されて、ガンでないのに陽性が出てしまう率が1％になったと仮定して計算しなおしてみましょう。その他の数値は変えません。すると、
約8.7％となりました。精度が高くなっています。
しかし、尤度が95％で変わっていないので、やはり1000人のうち50人はガンなのに見逃されています。そこで、検出精度の方を上げてみます。より敏感な試薬を使う感じです。95％を98％に変えてやってみましょう。（はずれ陽性率は元の2％に戻します。）
約4.7％となりました。元の状態とあまり変わりませんね。が、少し精度が上がっています。
ベイズ推定のすぐれた特徴に、実は「柔軟性」があります。上のような「はずれ陽性率」や「見落とし陰性率」といったものは、新しい試薬を導入した直後だと、あまりあてにならない数値しかえられない場合もあるでしょう。多少時間をかけたデータの蓄積を経ないと精度が上げられない、とか。
そういう場合でも、「ある程度の数値」を与えておけば、「それなりの条件付き確率が計算できる」、つまりそれなりの答えが出せるのです。
世にあるたいていの数式は、パラメーターに未知数や間違いがあると、答えが出せないか、意味のない答えしか出せません。しかし、ベイズ推定は、多少あてにならない数値があったとしても、真の答えからそう遠くへだたってはいない答えが出せます。
極端にいえば、「だいたい○％くらいじゃないかな」という主観的な値を尤度（もっともらしさ）を与えても、何もないよりは助かる目安にはなりうる条件付き確率が得られるということです。怪しい数値は、あとになってからより実態に近い数値に置き換えて計算すれば良いのです。上で試してみたように。
そのように、条件確率などのパラメーターを変えて計算し直すことを「ベイズ改訂」といいます。
ベイズ改訂を少しずつ重ねることで、より実態に即した確率が得られていくことが期待できます。ということは、これもまたヒューリスティックな確率探索のプロセスに利用できる、ということです。
つまるところ、ベイズ推定は人工知能にバッチリ使えるってわけです。
では、次の記事ではベイズ推定の人工知能への応用をみていきます。
