人工知能の歴史・理論と技術 2
それでは、第1次AIブームでの人工知能研究の展開を押さえます。
第1次AIブーム・「古き良き人工知能」 1956~1974年頃
ダートマス会議後、しばらくの間、人工知能は驚異の目で注目を浴びました。コンピュータが代数の問題を解き、幾何学の定理を証明し、簡単な英会話を学習するなど、多少なりとも「知的」な動作を見せることが、当時の多くの人々にとっては驚くべきことだったのです。
この時期の成果を見ていきます。
1957 A. Newell,J. C. Shaw,H. SimonがGeneral Problem Solver(GPS)を開発
GPSは汎用の問題解決プログラムとして開発されました。このプログラムは、手段目標分析 Means-Ends Analysis (MEA)にもとづいて問題を解決します。
たとえば、迷路の入口から出口まで進むという問題をGPSに与えます。まずGPSは現在の位置(現在状態)とゴールの位置(目標状態)を確認、評価します。次に、現在状態と目標状態の差を縮めるための行動をとります。すると新しい現在状態が生まれます。これと目標状態を評価し、次の行動をとり……というサイクルを繰り返します。
もしも行動の結果、現在状態が前よりも悪くなったり、行き止まりに当たって進めなくなったりしたら、前の行動選択分岐のステップにさかのぼって、やりなおします。このように、最初から正解のルートを考え出すのではなく、一歩一歩暫定的な解を出して試行錯誤を重ねるやり方をヒューリスティック heuristicといいます(「探索ヒューリスティック法」ということもあります)。
こうしたアルゴリズムは、迷路のほか、チェス、代数や幾何の証明などにも応用されました。
1958 J. McCarthyがプログラミング言語LISPを開発
コンピュータが直接受け取って実行するコマンドは2進数で表現される「機械語」ですが、あるまとまった処理を人間の言葉に近いコマンド、ステートメント、パラメーターで記述できるようにしたものを「高級言語」、または「高水準言語」と言います。LISPはFORTRANに次いで2番目に古い高水準プログラミング言語です。
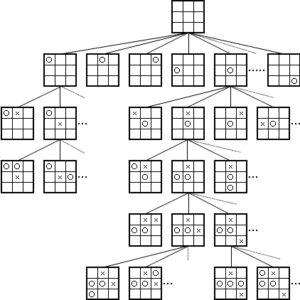
上記の迷路、チェス、証明問題は、ヒューリスティックによる暫定解の分岐がツリー状の構造(探索木)になっていきますが、LISPはこのようなツリー状構造の演算を得意としており、今でも人工知能プログラムを記述する有力な言語として使われています。
http://hitsujiai.blog48.fc2.com/blog-category-4.html
1958 J. McCarthyがAdvice Takerを作成
Advice Takerは、「事前知識を豊富に与えられ、自動演繹を行うプログラムは、常識をそなえている」という性格を持つAIプログラムでした。「アドバイスを受け取る」ことができるプログラムで、稼働しながら新しい知識(公理や定理)を受け入れ、推論―応答の精度、確かさを改善できる仕組みでした。
医療における診断などに応用できるエキスパートシステム、既知の公理系と定理から新しい定理を証明する自動推論などの元となりました。
1958 Friedbergが遺伝的アルゴリズムの原型・機械進化の実験を行う
遺伝的アルゴリズム Genetic Algorithm とは、生物の進化にならい、遺伝と適者生存(自然淘汰)をソフトウェア的に再現することで、複雑な問題に対する最適解を探索、近似していく手法です。ある問題に対する解の候補を遺伝子で表現した「個体」として複数用意し、適応度の高い個体を優先して交配し、突然変異も時々起こさせる操作を繰り返しながら、最適解の探索をおこないます。
1960 B. Widrowがニューラルネットワークを改良
1962 F. Rosenblattがニューラルネットワークで単純パーセプトロンを開発(論文は1958年)
ミンスキーとエドモンズが作ったSNARCがニューラルネットワークの原型となりましたが、ローゼンブラットは人工ニューロン Artificial Neuronを使って入力層と出力層からなる単純パーセプトロン Simple Perceptron を作りました。
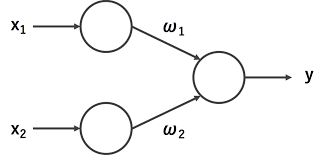
パーセプトロン
パーセプトロンでは、1つの人工ニューロンが複数の入力を受け、それぞれに重み付け weighting をし、重みを合計した値があらかじめ決められた閾値を越えていたら「1」、越えていなかったら「0」を出力します。
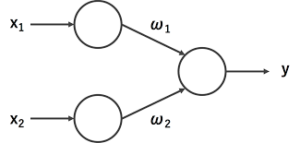
ここでは単純化して、入力をx1、x2の2つ、それぞれに対する重み付け値をw1、w2、閾値をt、出力をyとします。入力側に2つのニューロンがあり、これが1つのニューロン(出力層ニューロン)につながっている形です。
http://miyamo765.hatenadiary.jp/entry/2017/04/26/
このパーセプトロンに、論理関数の AND (論理積)を学習させましょう。ANDの真理値は以下の通りです。
| No | x1 | x2 | y |
| 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 0 | 1 | 0 |
| 4 | 1 | 1 | 1 |
これが目標となる正解です。
出力層ニューロンの重み付け値w1、w2、および閾値tはランダムな初期値をとるものとし、No.1からNo.4までの入力パターンすべてに対して正しいyを出力するようになるまで、変えていきます。すべて正しいyを出力するようになったら、学習成功です。
では仮に、(w1, w2, t)= (0.5, 1, 0.7) としてスタートしましょう。x1×w1+x2×w2を計算した値がtを越えたらy=1、越えなかったらy=0が出力されます。
No.1 0×0.5+0×1=0
x1=0、x2=0、y=0となり、上の真理値に合致するので、OKです。
No.2 1×0.5+0×1=0.5 t>0.5なのでy=0
x1=1、x2=0、y=0で、OKです。
No.3 0×0.5+1×1=1 t<1なので、出力y=1です。
x1=0、x2=1、y=1となり、ここは不正解。
No.4 1×0.5+1×1=1.5 出力y=1
x1=1、x2=1、y=1で、OKです。
No.3のパターンでだけ、失敗しました。
ここで失敗の原因を反省してみますと、No.3の「入力x2だけが1になっている」ところでつまづいていることがわかりますので、x2に対する重み付け値w2に問題がありそうだと思い至ります。そこでw2を0.6まで小さくしてみます。そうしてNo.3を計算しますと、
0×0.5+1×0.6=0.6 t>0.6なのでy=0
となり、x1=0、x2=1、y=0で正解になりました。No.1、No.2、No.4についても問題ありません。
こうして、このパーセプトロンは論理積ANDを学習しました。
同様のやり方で、論理和ORや否定論理積NANDといった論理関数も単純パーセプトロンは学習可能です。
ただ、1968年にミンスキーは単純パーセプトロンの限界を指摘します。AND、OR、NANDといった線形分離可能なものしか学習できず、排他的論理和XORなど線形分離不可能な関数は学習できないという指摘です。
「こんなこともわからないの……」という失望が広がり、第1次AIブームが終わり冬の時代に入る大きな要因になりました。
線形分離可能というのは、論理関数の真理値を平面上に表したとき、y=1の領域とy=0の領域を、平面よりひとつ低い次元の直線で区切ることができるということです。例えばANDでは、
(x1)
2 ④
1 3 (x2)
となり、2-3と④の間に直線が引けます。(数字は真理値表のNo.1から4にあたり、丸数字がy=1のもの、○なし数字はy=0を表します。)
論理和ORでは、
(x1)
② ④
1 ③ (x2)
となって、やはり②―③と1の間に線が引けます。
これに対し、排他的論理和XORでは、
(x1)
② 4
1 ③ (x2)
となり、区切る線を引こうとすればどうしても曲線になってしまいます。
単純パーセプトロンでは、こうした関数は学習できないということです。
この頃は、処理速度やメモリーの容量などの面でコンピュータの能力が低かったことも、この問題が深刻に受け止められた背景にあります。
のちに1986年になって多層パーセプトロン Multilayer Perceptronが開発されると、この問題は解決されました。そしてこの多層パーセプトロンが、ディープラーニングを可能にするニューラルネットワークにつながっていきます。
さて、次の記事では引き続き第1次AIブームについて書きますが、主にその終わりと冬の時代に触れていきます。次の記事の中心トピックは「フレーム問題」です。