遺伝的アルゴリズム
1975年にジョン・ホランドによって提案されたアルゴリズムです。生物の進化をモデルに、解の候補となるデータ(遺伝子)を持った個体を多数用意し、問題に適用、適応度の高い個体を優先的に選択し、遺伝子の一部を交叉させ、次の世代の遺伝子とします。適応度の低い個体は自然淘汰になぞらえて抹殺されます。それにより減った数だけ、次の世代の個体が補充され、全体の個体数は変わりません。また一定の確率で突然変異も起こるように設定されます。大筋の流れは以下のとおりです。
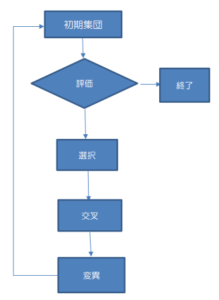
遺伝的アルゴリズムは幅広くさまざまな問題に適用可能ですが、特に以下のような問題に向いています。
・巡回セールスマン問題のように、要素数が増えると組み合わせ爆発により計算量が膨大になる問題
・新幹線の先端部分の形状のように、ある程度やってみないとわからない問題
・そもそも解が存在するのかどうかもわからない問題
では、上のフローチャートに示した処理ポイントを見ていきます。巡回セールスマン問題を例にします。巡回セールスマン問題とは、いくつかの都市をすべて巡回するとき、移動距離が最短となる移動順を決めていく問題で、都市の数が増えると順序の組み合わせ数が膨大になる「NP困難」とされます。都市の数が30を超えると、スーパーコンピュータでも何兆年も時間がかかるような理論計算難易度です。
初期集団――遺伝子の設計が最重要
セールスマンをたくさん用意します。マシンのパワーによってはあまり多くすると時間がかかってしまいますが、だいたい50人とか100人とか、そのくらい雇います。使えない奴はどんどんクビにしていきますし、最終的には一番使える奴以外はすべてクビにしますから大丈夫です。
初期集団の設定でもっとも重要なのは遺伝子の設計です。巡回セールスマン問題では、都市をめぐる順番を表現する遺伝子を考えればいいのですが、たとえば都市が5つの場合、
1-1 15324 ※「1-1」は「第一世代のセールスマン1号」、「15324」は都市の番号と順序
1-2 23154
1-3 35421
のように設計するとマズイことが起こります。
というのは、仮に「1-1」と「1-2」の適応度が高かったとすると、このふたりを選択して遺伝子の交叉をするのですが、たとえば遺伝子の第3座以降を入れ替えると、
2-1 15154
2-2 23324
となります。おわかりでしょうか。「2-1」は都市1と都市5を2回も訪問しますが、都市2と都市3には行かないことになり、「2-2」は都市2と都市3に2度行き、都市1と都市5には行かないのです。これでは両名とも即刻クビで、良い遺伝子を継ぐことができていません。つまり即死遺伝子になってしまいます。
そこで一工夫して、
1 → 2 → 3 → 4 → 5 (都市の番号順)
0 1 2 3 4
というふうに、都市番号の小さい順に0から4のコードを対応させ、「都市番号順の通りなら0、入れ替わるときはその都市番号に対応するコードをあてはめる」という約束で遺伝子を作ります。
するとたとえば、「1-1」の「15324」は、
① 先頭はいちばん小さい1なので、遺伝子コードは0
② すると都市番号2、3、4、5に0、1、2、3とコードが振り直される
③ 1-1の遺伝子第2座は5なので、遺伝子コードは3
④ 都市番号2、3、4に遺伝子コード0、1、2を振り直し
⑤ 遺伝子第3座は3なので、遺伝子コードは1
⑥ 都市番号2、4に遺伝子コード0、1を振り直し
⑦ 遺伝子第4座は2なので、遺伝子コードは0
⑧ 残る都市番号4はコード0なので、遺伝子第5座も0
ということで、「1―1」の遺伝子は「03100」となります。
この方式だと「12345」は「00000」になり、「13245」は「01000」になります。この形にすると、即死遺伝子は生じにくくなります。
とにかく、遺伝的アルゴリズムでいちばん重要なのは「遺伝子の設計」です。
評価
次に100人なら100人のセールスマンに、実際に5都市を巡回させます。全員の巡回が終わったら、移動距離を比較します。この場合、短ければ短いほど優秀です。
選択
評価にもとづいて、第2世代に残すセールスマン、遺伝子を交叉させるセールスマン、そしてクビにするセールスマンを選択します。いくつかの代表的な方式を紹介します。
ルーレット選択
成績が優秀なほど選択される確率が高くなり、悪くなるほど確率が低下する方式。
巡回セールスマン問題では移動距離が短いほど優秀なので、その逆数をとってすべて合計し、この合計値を分母にしてひとりひとりの移動距離逆数を割ってやれば、それぞれが選択される確率が算定されます。
イメージとしては、円グラフ上に各個体の成績を扇形で描き(優秀な個体ほど広くなる)、円グラフを回してダートを投げて刺さったところの個体を選び出していく感じです。
ランキング選択
「1位ならば80%、2位ならば75%、3位ならば70%……」といったように、順位ごとに選択確率を固定して設定する方式。
トーナメント選択
全体の中からあらかじめ決めた数の個体を抜き出し、その中から適応度の高い個体を選ぶ方式。
エリート選択
適応度が上位の個体を一定数、次の世代にそのまま残し、それより下位の個体は交叉、抹殺の対象にする方式。
解の収束が速くなる傾向のある方式ですが、反面遺伝子の多様性が失われやすく、局所最適解におちいる危険性もあります。
以上のような選択方法で次世代に引き継ぐ個体を選びます。最下位から20人くらいは、クビでいいでしょう。
遺伝子の交叉
続いて遺伝子の組み換え、交叉を行います。これにもいくつかの方式があります。
一様交叉
遺伝子を入れ替える遺伝子座位を指定するフィルタを使う方式。たとえばフィルタ「01100」なら、個体Aと個体Bそれぞれの遺伝子第2座と第3座のみを入れ替えます。
一点交叉
ふたつの個体の遺伝子の途中の一点をランダムに決め、そこよりも後の遺伝子を入れ替える方式。
二点交叉
遺伝子の途中にランダムに2点を決め、その間の遺伝子を2個体間で入れ替える方式。3点以上で区切って交叉する方式を多点交叉といいますが、あまり使われません。
一点交叉や二点交叉と、一様交叉を組み合わせる方式もあります。
変異(突然変異)
一定の確率で、各個体の遺伝子は突然変異を起こします。生物界に見られる突然変異をモデル化しています。生物界での突然変異は、遺伝子の多様性を保ち、環境の変化に種が対応する可能性を高める作用をします。遺伝的アルゴリズムにおいても同様で、世代交代が進むうちに遺伝子が一様になり、局所最適解におちいってしまうのを避けるために、一部の個体の遺伝子にランダムに変化を加えます。
遺伝的アルゴリズムで突然変異が起きる確率は、高くても1%程度に設定されます。確率が低すぎると局所最適解におちいりやすくなり、高すぎるとランダム探索に近くなって解が収束しにくくなります。
突然変異が生じた個体はほとんどの場合、生存に適さない即死遺伝子になりますが、まれに優秀な成績をおさめる個体になることもあります。
遺伝的アルゴリズムの問題点
前述のように、遺伝子の設計が最重要ですが、それがクリアできても、
・選択の方式、選択個体数、選択確率をどう設定するか
・交叉の方式、交叉の範囲をどう設定するか
・突然変異の方式、確率をどう設定するか
といったさまざまなパラメーターの設定により、遺伝的アルゴリズムの出来不出来が左右されます。今のところ、プログラマーの経験と勘、すなわち「職人技」が求められる場合がほとんどです。選択、交叉、突然変異のパラメーター設定を遺伝子とする遺伝的アルゴリズムを組んで(いわばメタ遺伝的アルゴリズム)、最適な遺伝的アルゴリズムを探索することも、やろうと思えばできるでしょうが、そのメタ遺伝的アルゴリズムも最適化するには職人技とセンス、あるいはメタメタ遺伝的アルゴリズムが必要になり……と、話がメタメタになってきりがありません。
うまくいく遺伝的アルゴリズムを作るには、結局トライ&エラーを繰り返し、出来の悪い遺伝的アルゴリズムの屍を累々と重ねるしかないわけです。これはもう、人力遺伝的アルゴリズムですね。
ルーレット選択の設定が甘かったり、突然変異の効果が低すぎたりすると、初期収束という問題が起こります。ごく早い段階で探索が収束してしまい、それがえてして局所最適解にあたってしまうのです。
これを避けるには、各種パラメーターの設定を改善するしかありません。
また、一点交叉や二点交叉の場合、遺伝子のコード長が長くなればなるほど、最適解に収束していく確率は低くなり、したがって実行時間は長くなっていきます。
一様交叉ではこうした問題は起こりにくくなりますので、交叉方式は一様交叉が効率的と言えるでしょう。
まとめ
遺伝的アルゴリズムは、適用できる問題の範囲が非常に広く、マトモに引き受ければ膨大な計算量になる問題にもヒューリスティックな手法で取り組める、非常に強力なアルゴリズムです。人工知能のヒューリスティック部門を代表する技術と言えるでしょう。
さて、次の記事でも引き続きヒューリスティックな手法のアルゴリズムを紹介します。


